유리 베가
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
유리 베가는 슬로베니아 출신의 수학자, 물리학자, 포병 장교이다. 그는 1783년에 로그 표 시리즈를 출판했고, 1789년에는 원주율을 140자리까지 계산하여 세계 기록을 세웠다. 군 복무 중에는 여러 전쟁에 참전했으며, 1802년 다뉴브 강에서 익사한 채 발견되었다. 그의 업적을 기리기 위해 슬로베니아의 여러 기관과 장소, 천체 등이 그의 이름을 따 명명되었고, 우표와 주화가 발행되었다.
더 읽어볼만한 페이지
- 슬로베니아의 수학자 - 요제프 슈테판
오스트리아의 물리학자, 수학자, 시인이었던 요제프 슈테판은 빈 대학교에서 물리학을 가르치며 흑체 복사 법칙을 발견하고 기체의 열전도율을 최초로 측정하는 등 다양한 분야를 연구하여 그의 업적을 기리는 연구소와 분화구가 명명되었다.
2. 생애 초반
유리 베가는 슬로베니아 류블랴나 동쪽에 위치한 작은 마을인 자고리차에서 농민 가정의 아들로 태어났다.[9][2] 그가 6세였을 때 아버지 예르네이 베가가 사망했다.
빈 포병학교 수학 교수로 임관하며 1780년부터 군 복무를 시작했다. 이 시기부터 성씨를 '베하'(Veha) 대신 '베가'(Vega)로 사용하기 시작했다. 33세 되던 해에는 당시 16세였던 체코 체스케부데요비체 출신의 귀족 요제파 스보보다(Jožefa Swoboda, 1771년–1800년)와 결혼했다.
유리 베가는 18세기 후반 수학 분야에서 중요한 기여를 남겼다. 그의 주요 업적은 로그 표를 개선하고 확장한 것과 원주율 계산 분야에서 두드러진다.
베가는 처음에는 모라브체에서 교육을 받았고, 1767년부터 1773년까지 6년 동안 류블랴나에 위치한 예수회 계열 고등학교(류블랴나 예수회 대학)에서 공부했다. 당시 약 500명의 학생이 있었으며, 베가는 라틴어, 그리스어, 종교, 독일어, 역사, 지리학, 과학, 수학을 배웠다. 그는 슬로베니아의 작가이자 역사가인 안톤 토마시 린하르트와 학교 친구였다.
19세였던 1773년에 고등학교를 졸업하고 류블랴나의 리세움에서 학업을 이어갔다. 1775년에는 학업을 마치고 항해 기술자가 되었다.[10] 그의 종합 시험 문제 목록인 ''Tentamen philosophicum''은 류블랴나 수학 도서관에서 찾아볼 수 있으며, 이는 논리학, 대수학, 형이상학, 기하학, 삼각법, 측지학, 입체기하학, 곡선 기하학, 탄도학, 일반 및 특수 물리학 등 광범위한 주제를 다루었다.
3. 군 복무
그는 여러 전쟁에 참전했다. 1788년에는 오스트리아 제국의 원수 에른스트 기데온 폰 라우돈 휘하 부대에 합류하여 베오그라드에서 오스만 제국을 상대로 전투를 치렀다. 그가 지휘한 박격포 포대는 베오그라드 요새 함락에 크게 기여했다. 1793년부터 1797년까지는 오스트리아 장군 다고베르트 부름저가 이끄는 연합군에 속해 프랑스 혁명군과 싸웠으며, 포르 루이, 만하임, 마인츠, 비스바덴, 케흘, 디에츠 등 여러 전투에 참여했다. 1795년에는 원뿔형 구멍과 더 큰 장약을 사용하여 14kg 박격포의 최대 사거리를 3000m까지 늘리는 개량을 이루어냈다. 이는 기존 27kg 박격포의 사거리 1800m를 크게 넘어서는 것이었다.
1802년 9월 실종 신고가 접수되었고, 며칠간의 수색 끝에 시신으로 발견되었다. 경찰은 그의 죽음을 사고사로 결론지었다. 그는 1802년 9월 26일 오스트리아 빈 인근 누스도르프의 도나우강에서 사망한 것으로 추정된다.
4. 수학적 업적
그는 여러 로그표 관련 저서를 출판했으며, 특히 1794년에 출판된 《모든 로그의 창고》(Thesaurus Logarithmorum Completusla)는 그의 대표작이다. 이 로그표는 기존 표의 오류를 수정하고 정밀도를 높여 후대 수학자들에게 유용하게 사용되었다.
또한 베가는 1789년 원주율 값을 당시 세계 기록인 소수점 이하 140자리까지 계산했으며, 이 중 126자리까지 정확했다.[4] 그는 존 매친(John Machin) 등이 제시한 기존 원주율 계산 공식을 개선하여 계산 효율성을 높이는 데 기여했다.[5]
이 외에도 베가는 4권으로 구성된 수학 교과서 《수학 강의》(Vorlesungen über die Mathematikde)를 집필하여[3] 수학 교육에도 힘썼다. 이 교과서는 1782년부터 1800년에 걸쳐 출판되었으며, 흥미로운 수학 표와 공식을 담고 있었다. 그는 최소 6편의 과학 논문을 발표했으며, 탄도학, 물리학, 천문학 분야에서도 연구 활동을 수행했다.
1781년에는 오스트리아 합스부르크 군주국 내에서 미터법 도입을 주장하기도 했으나 당시에는 받아들여지지 않았다. 그의 학문적 성과는 여러 과학 아카데미 회원 자격 획득과 훈장 및 세습 남작 작위 수여 등으로 인정받았다.
4. 1. 로그표
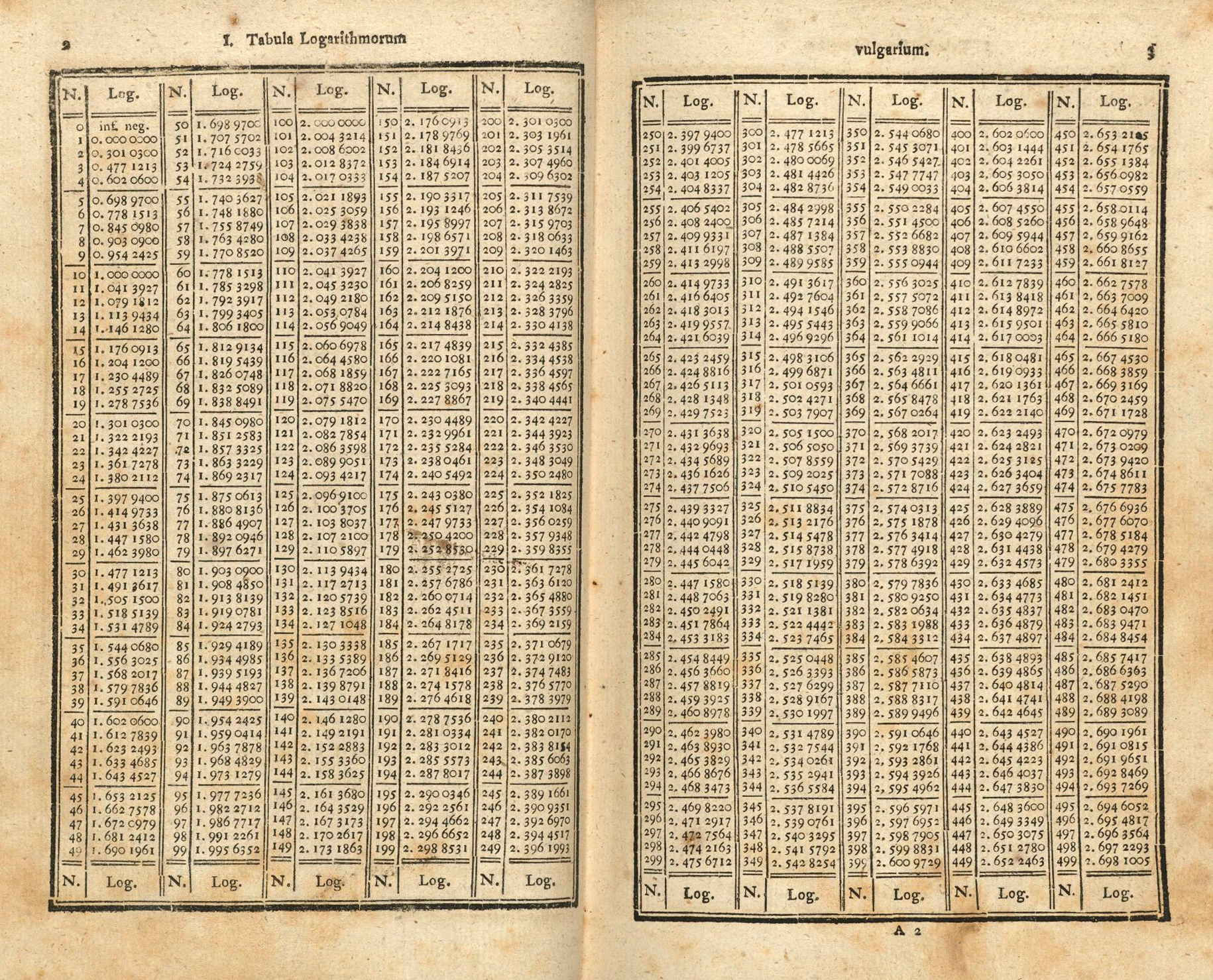
베가는 여러 권의 로그 표 시리즈를 출판했다. 첫 번째 책은 1783년에 나왔으며, 그의 주요 저서인 《모든 로그의 창고》(Thesaurus Logarithmorum Completusla)는 1794년 라이프치히에서 처음 출판되었다. 이 책은 1924년에 90번째 판이 나올 정도로 오랫동안 중요한 자료로 사용되었다. 이 수학 표는 네덜란드 수학자 아드리안 블라크(Adriaan Vlacq)의 표를 기반으로 했지만, 베가는 기존의 많은 오류를 수정하고 작은 각도에 대한 삼각 함수의 로그 값을 더 정밀하게 확장했다.
1793년에는 휴대하기 편한 수첩(핸드북) 형태의 로그표를 처음 출판했는데, 이는 이후 여러 언어로 번역되어 100종류 이상의 판본으로 출간될 정도로 널리 보급되었다. 1797년에는 적분과 여러 유용한 공식들을 모아 정리한 로그표 시리즈의 제2권을 출간했다.
베가의 로그표는 후대 학자들에게도 큰 영향을 미쳤다. 그라츠 공과대학교의 명예 평의원이었던 공학자 프랑크 알머(Franc Allmer)는 괴팅겐의 카를 프리드리히 가우스 박물관에서 베가가 만든 소수점 10자리 로그표를 발견했다. 독일의 위대한 수학자 카를 프리드리히 가우스는 이 로그표를 자주 사용했으며, 표 여백에 직접 계산한 내용을 적어두기도 했다. 가우스는 베가의 로그표를 검토하면서 백만 개 이상의 숫자 범위에서 몇 가지 계산 오류를 찾아내기도 했다. 또한, 영국의 수학자이자 컴퓨터 과학의 선구자인 찰스 배비지가 개인적으로 소장했던 베가의 《모든 로그의 창고》 초판본은 현재 에든버러 왕립 천문대에 보관되어 있다.
4. 2. 원주율 계산
베가는 1789년 8월 20일, 원주율(π) 값을 소수점 이하 140자리까지 계산하여 당시 세계 기록을 세웠다. 이 중 처음 126자리까지 정확했다.[4] 그는 이 계산 결과를 상트페테르부르크의 러시아 과학 아카데미에 제출했고, 이 과정에서 1719년 프랑스 수학자 토마스 판테 드 라니(Thomas Fantet de Lagny, 1660–1734)가 계산한 원주율 값의 113번째 자리에서 오류를 발견했다.[4] 베가가 세운 이 기록은 1841년까지 52년 동안 유지되었고, 그가 사용한 계산법은 오늘날에도 언급된다. 그의 계산 결과에 대한 논문은 아카데미에서 6년 뒤인 1795년에 출판되었다.[4]
베가는 원주율 계산을 위해 다음 공식을 사용하거나 개선했다. 그는 1706년 존 머친(John Machin)의 공식을 개선했고,[5]
:
1755년 레온하르트 오일러(Leonhard Euler)가 발표한 공식과 같은 형태의 공식을 사용하기도 했다.
:
또한, 허턴(Hutton)의 공식과 비슷하며 존 머친의 공식보다 빠르게 수렴하는 다음 공식을 활용했다.[5]
:
그는 급수의 두 번째 항을 한 번만 개발했다.
5. 유산
1901년 슬로베니아 이드리야에는 그의 이름을 딴 유리 베가 고등학교 Gimnazija Jurija Vegesl가 문을 열었다. 이 학교는 슬로베니아 최초의 실업학교이기도 하다. 1935년에는 달에 있는 베가 분화구에 그의 이름이 붙여졌다.
슬로베니아 국립은행은 1993년 3월 유리 베가를 기리는 50SIT 지폐를 발행했으며,[6] 슬로베니아 우정청은 1994년 그를 기념하는 우표를 발행했다. 2004년에는 슬로베니아가 그의 탄생 250주년을 기념하는 동전을 발행하기도 했다.[7] 1997년 7월 30일에 발견된 소행성 14966 유리베가 역시 그의 이름을 따서 명명되었다.
슬로베니아의 베가 천문학회[8]는 유리 베가와 별 베가의 이름을 함께 따서 지어졌다.[15] 다만, 별 베가의 이름 자체는 유리 베가와는 관계없이 훨씬 이전부터 사용되던 이름이다. 또한 3D 변형 가능 객체 시뮬레이션을 위한 무료 오픈 소스 물리학 라이브러리인 베가 FEM(Vega FEM)도 그의 이름을 따서 명명되었다.
6. 과학적 계보
베가는 오스트리아의 수학자인 Ignaz Lindner|이그나츠 린트너de의 가정교사이자 학문적 지도자였으며,[10][1] 이로 인해 주목할 만한 과학 계보가 형성되었다.
참조
[1]
문서
Georg Vega, Slovenian Archimedes (from Pasture to Baron)
https://www.academia[...]
[2]
서적
Die Völker Oesterreich-ungarns. Ethnographische und culturhistorische Schilderungen
https://books.google[...]
K. Prochaska Press
[3]
웹사이트
Vorlesungen Vorlesungen über die Mathematik - wikimedian commons
https://commons.wiki[...]
[4]
저널
Detérmination de la demi-circonférence d'un cercle dont le diameter est = 1, exprimée en 140 figures decimals
https://archive.org/[...]
[5]
웹사이트
hutton's formula - from Wolfram Mathworld
https://mathworld.wo[...]
[6]
웹사이트
Slovenia 50 tolarjev banknote 1992 Baron Jurij Bartolomej Vega
https://www.worldban[...]
[7]
웹사이트
250th anniversary of the Birth of Jurij Vega (2004)
https://www.bsi.si/e[...]
[8]
웹사이트
Astronomsko društvo Vega
https://www.ad-vega.[...]
[9]
서적
Die Völker Oesterreich-ungarns. Ethnographische und culturhistorische Schilderungen
https://books.google[...]
K. Prochaska Press
[10]
웹인용
'"Georg Vega, Slovenian Archimedes (from Pasture to Baron)'
https://www.academia[...]
[11]
웹인용
Vorlesungen Vorlesungen über die Mathematik - wikimedian commons
https://commons.wiki[...]
[12]
저널
Detérmination de la demi-circonférence d'un cercle dont le diameter est = 1, exprimée en 140 figures decimals
https://archive.org/[...]
[13]
웹인용
hutton's formula - from Wolfram Mathworld
https://mathworld.wo[...]
[14]
웹인용
Physicists on Banknotes Page Two
http://www-personal.[...]
2023-04-10
[15]
웹인용
Astronomsko društvo Vega
https://www.ad-vega.[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com